计数排序(Counting Sort)算法介绍
一、引言
计数排序(Counting Sort)是一种基于哈希的排序算法。它通过统计每个元素的出现次数,然后根据统计结果将元素依次放入排序后的序列中。计数排序特别适用于元素范围较小的情况,例如整数范围在 0 到 k 之间。
二、算法思想
计数排序的核心是创建一个计数数组,用于记录每个元素出现的次数。具体步骤如下:
- 初始化计数数组:创建一个长度为最大元素值加 1 的计数数组,所有元素初始化为 0。
- 统计元素出现次数:遍历原始数组,将每个元素的值作为索引,在计数数组中对应位置加 1。
- 清空原数组。
- 根据计数数组排序:遍历计数数组,按照计数数组中的计数值将元素放回到原数组中。
三、动图演示
计数排序完整排序过程如下图所示:
演示说明: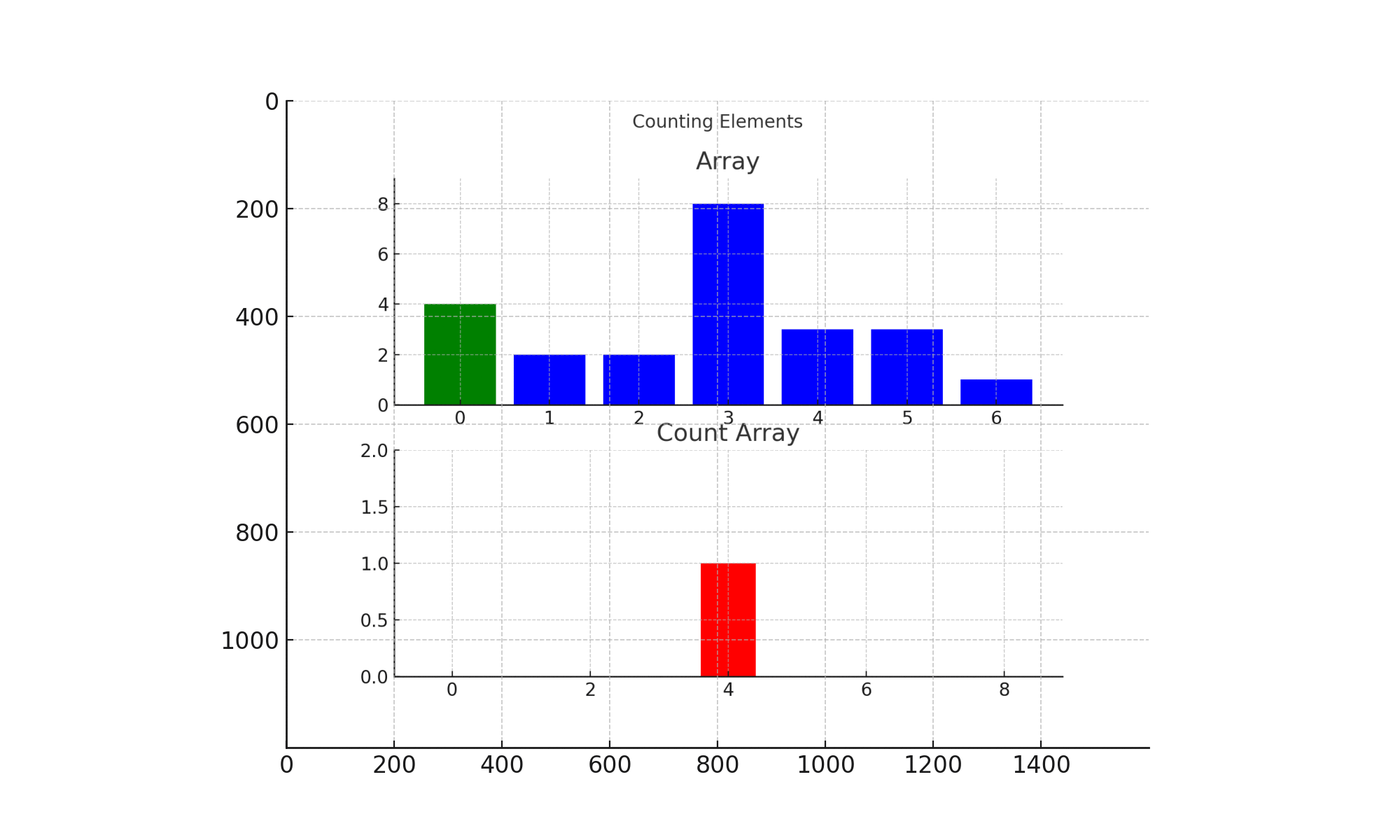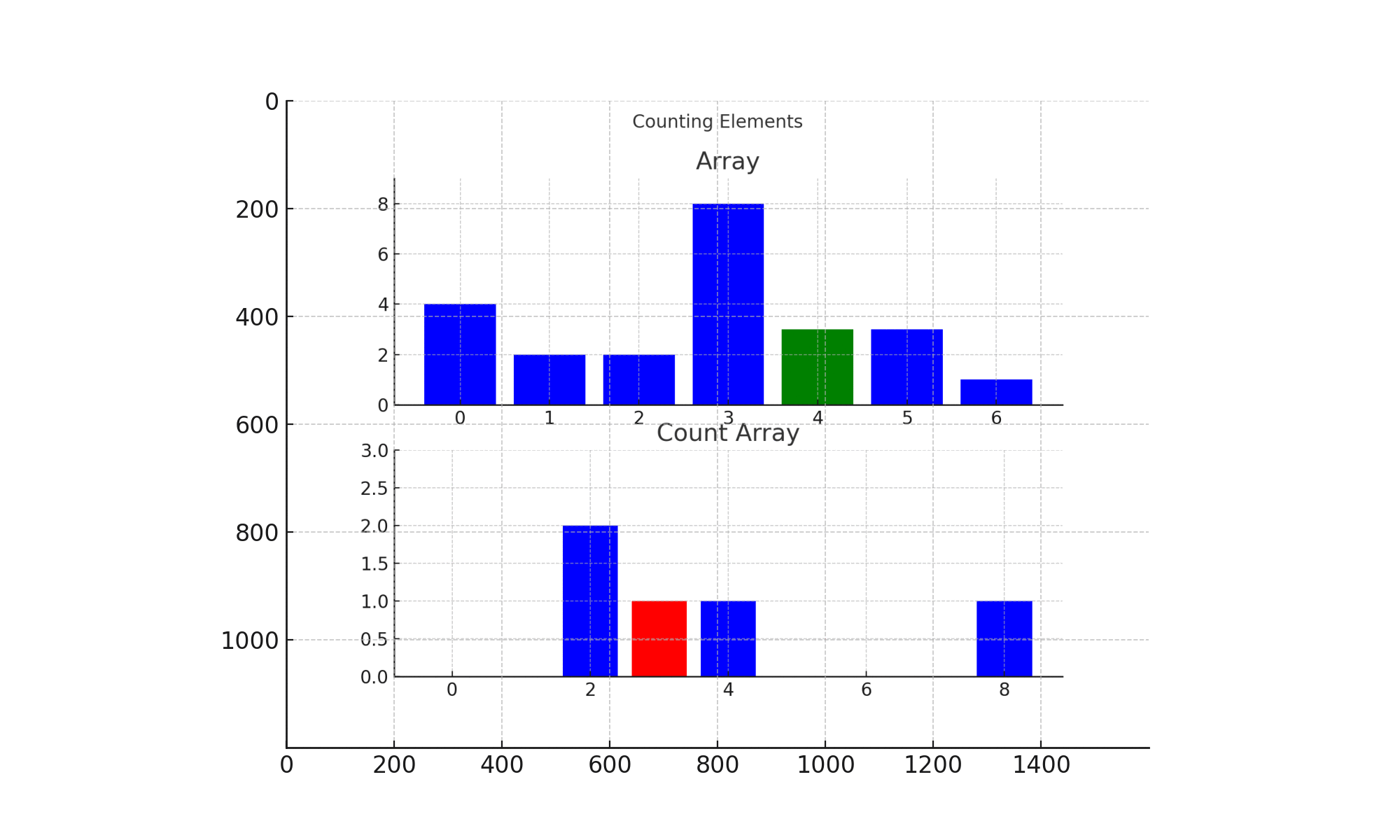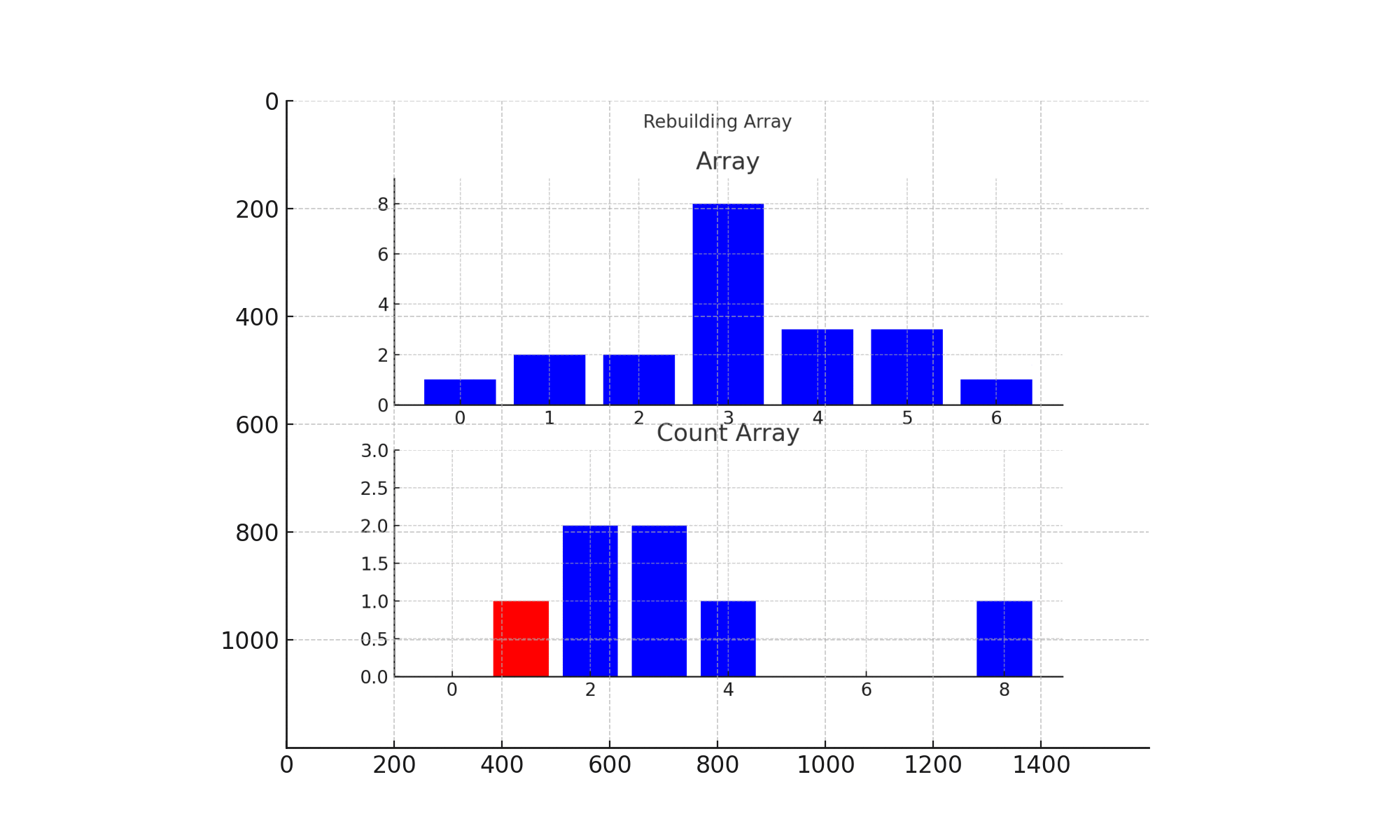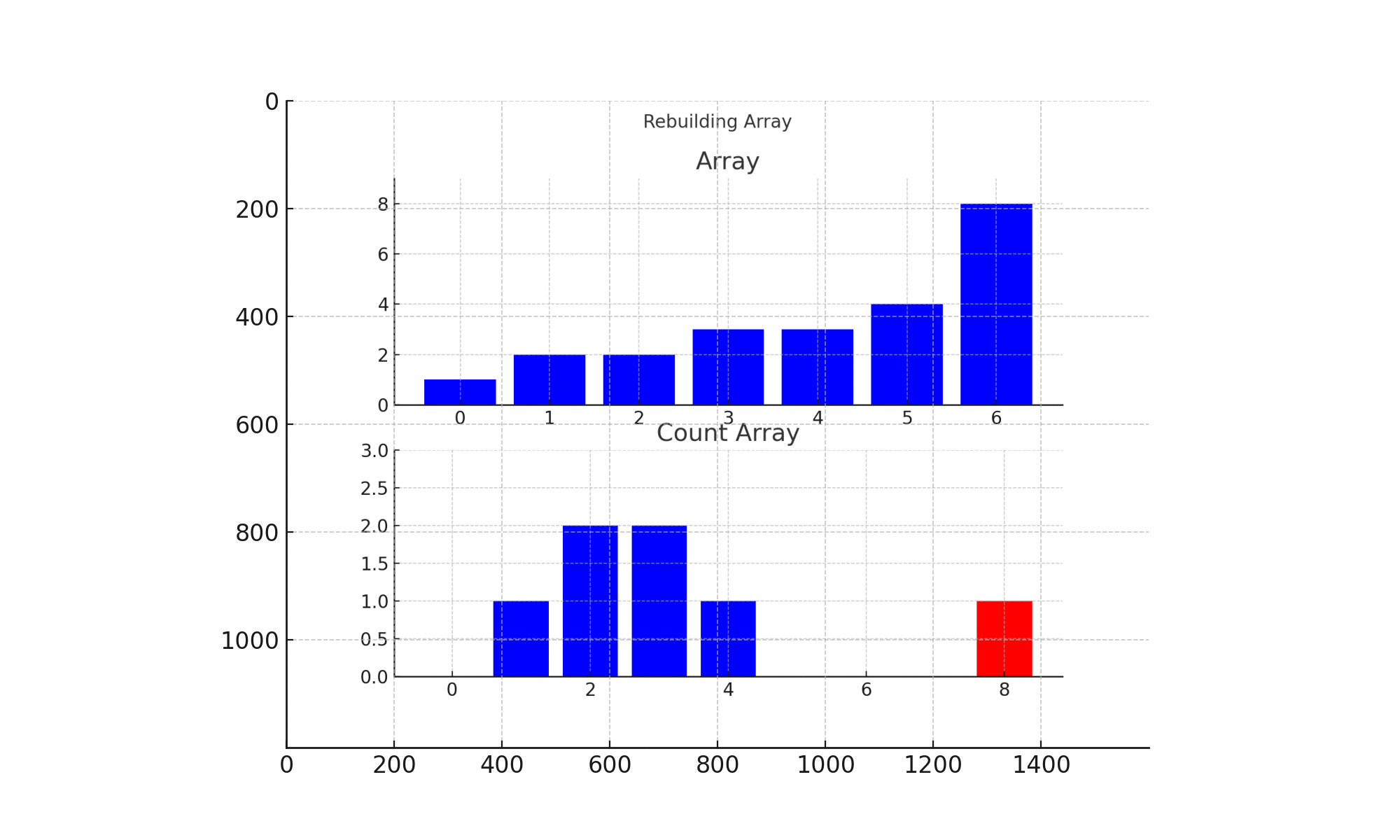
- 首先,程序生成一个范围为 [1, 9] 的计数数组,并且一开始所有值的计数都为 0。
- 然后,遍历原数组的所有元素,在对应的计数器位置执行计数操作。
- 最后,遍历计数数组,按照计数值将元素放回到原数组中。这样,所有元素都按照升序排列。
四、算法分析
1. 时间复杂度
假设一次「哈希」和「计数」的时间复杂度均为 O(1),并且总共有 n 个数,数字范围为 1 → k。计数排序中总共有四个循环:
- 初始化计数数组:时间复杂度 O(k);
- 枚举所有数字并计数:时间复杂度 O(n);
- 枚举所有范围内的数字:时间复杂度 O(k);
- 将元素放回原数组:时间复杂度 O(n)。
总的时间复杂度为:O(n + k)。
2. 空间复杂度
假设最大的数字为 k,则空间复杂度为 O(k)。
五、算法的优点
- 简单易懂:计数排序的原理非常简单,容易理解和实现。
- 时间复杂度低:对于范围较小的元素,计数排序的时间复杂度非常优秀。
- 适用于特定场景:当元素的范围已知且较小时,计数排序可以高效地完成排序。
六、算法的缺点
- 空间开销:计数排序需要额外的空间来存储计数数组,当元素范围较大时,可能会消耗较多的内存。
- 局限性:计数排序只适用于元素范围较小的情况,对于大规模数据或元素范围不确定的情况并不适用。
七、优化方案
计数排序在众多排序算法中效率较高,时间复杂度为 O(n + k)。然而,它的缺陷是非常依赖数据范围,必须为整数且限定在 [1, k] 范围内。因此,优化点主要集中在常数优化上:
- 初始化计数数组可以采用系统函数(例如 C/C++ 中的
memset,纯内存操作,优于循环)。 - 当排序元素达到 n 个时,可以提前结束第三个循环,跳出循环。