快速排序(Quick Sort)算法介绍
一、引言
快速排序(Quick Sort)是一种分而治之的排序算法。它通过选择一个基准元素,将数组分为两部分,一部分的元素都比基准小,另一部分的元素都比基准大,然后对这两部分再进行快速排序,最终得到有序的数组。
二、算法思想
快速排序的执行过程可以用以下几步描述:
- 选择基准元素:从数组中选择一个元素作为基准。
- 分割数组:将比基准小的元素放在基准的左边,比基准大的元素放在基准的右边。
- 递归排序:对基准左边和右边的子数组分别进行快速排序。
重复步骤 1 至 3,直到子数组的长度为 1 或 0。
三、动图演示
快速排序完整排序过程如下图所示:
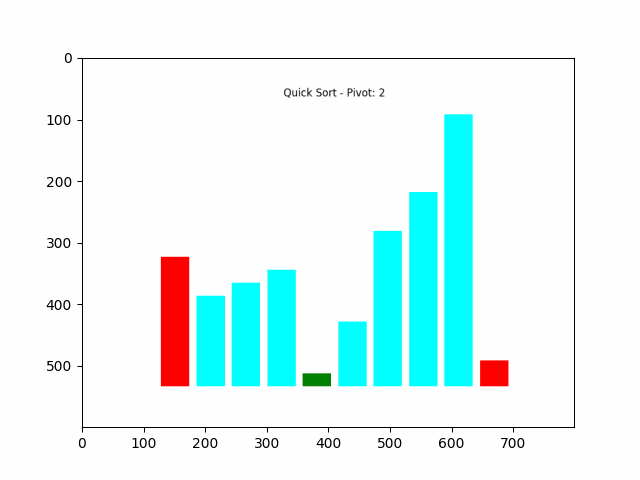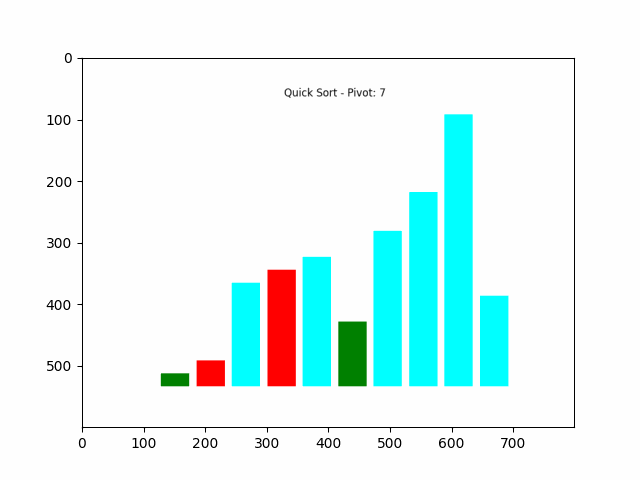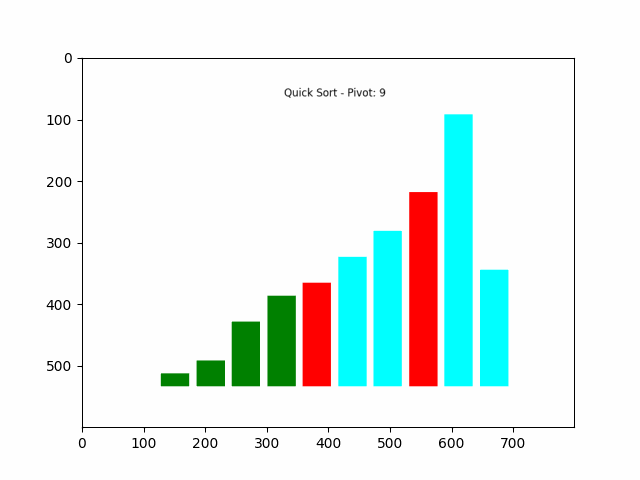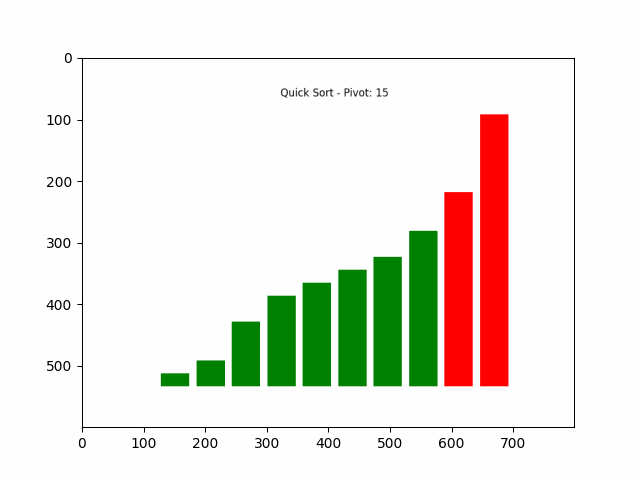
演示说明:
- 首先随机选择一个基准数,并将其与最左边的数交换。
- 然后从前到后依次遍历,判断小于基准数的元素为绿色,大于基准数的元素为紫色。
- 遍历完毕后,将基准数与“下标最大的那个比基准数小的数”交换位置。此时,基准数左边的数都小于它,右边的数都大于它。
- 左边和右边的数继续递归求解即可。
四、算法分析
1. 时间复杂度
- 最优情况:当每次选择的基准元素正好将数组分成两等分时,时间复杂度为 O(nlogn)。
- 最坏情况:当每次选择的基准元素是最大或最小元素时,时间复杂度为 O(n^2)。
- 平均情况:在平均情况下,时间复杂度也是 O(nlogn)。
2. 空间复杂度
快速排序的空间复杂度是 O(logn),因为在递归调用中需要使用栈来存储中间结果。这意味着在排序过程中,最多需要 O(logn) 的额外空间来保存递归调用的栈帧。
五、算法的优点
- 高效性:快速排序在大多数情况下具有较高的排序效率。
- 适应性:适用于各种数据类型的排序。
- 原地排序:不需要额外的存储空间。
六、算法的缺点
- 最坏情况性能:在最坏情况下,快速排序的时间复杂度可能退化为 O(n^2)。
- 不稳定性:快速排序可能会破坏排序的稳定性,即相同元素的相对顺序可能会改变。
七、优化方案
- 选择合适的基准:选择合适的基准元素可以提高算法的性能。
- 三数取中:通过选择中间元素作为基准,可以避免最坏情况的出现。
- 分区的改进:可以使用双指针或其他方法来改进分区的过程,提高算法的效率。
- 小数组使用插入排序:对于小数组,可以直接使用插入排序,避免不必要的递归。