选择排序(Selection Sort)算法详解
一、引言
选择排序(Selection Sort)是一种简单直观的排序算法。它的基本操作是从未排序序列中找到最小(或最大)元素,存放到已排序序列的末尾。重复这一过程,直到所有元素均排序完毕。
二、算法思想
- 第一步:在未排序序列中找到最小(或最大)元素,存放到排序序列的起始位置。
- 第二步:再从剩余未排序元素中继续寻找最小(或最大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。
三、动图演示
选择排序完整排序视频可以直观展示排序过程。关键步骤如下:
- 从第一个元素到最后一个元素中选择出一个最小的元素,与第一个元素进行交换。
- 从第二个元素到最后一个元素中选择出一个最小的元素,与第二个元素进行交换。
- 重复上述过程,从第 (i) 个元素到最后一个元素中选择出一个最小的元素,与第 (i) 个元素进行交换。
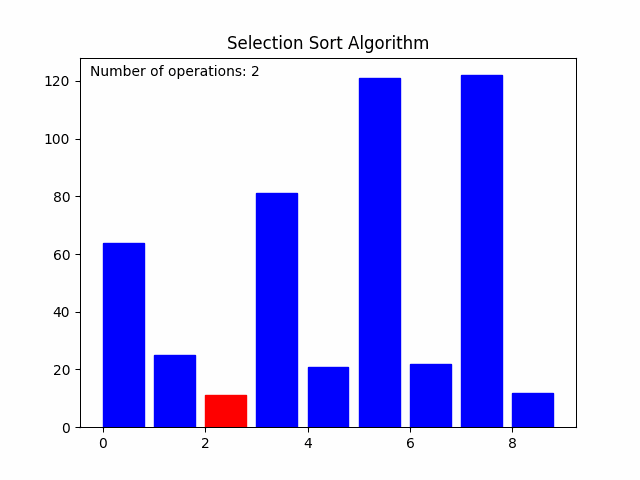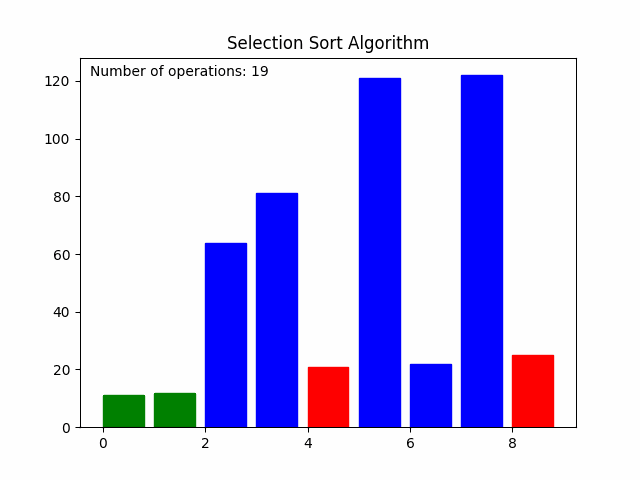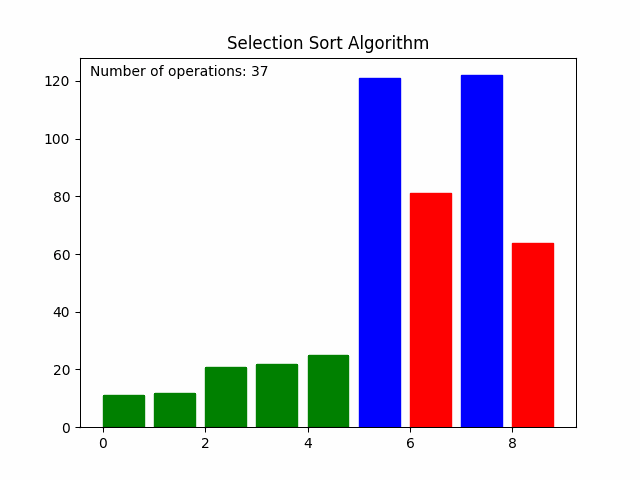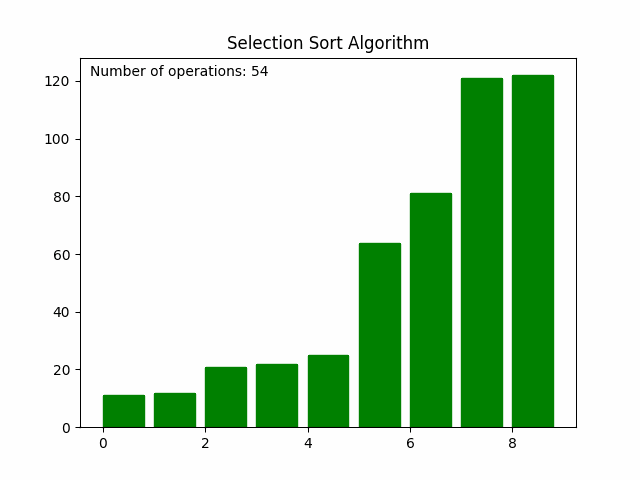
最终,所有元素将按照升序排列。
四、算法分析
1. 时间复杂度
选择排序的时间复杂度分析如下:
- 外循环运行 ( n - 1 ) 次迭代。
内循环的运行次数逐渐减少:
- 当 ( i = 0 ),内层循环进行 ( n - 1 ) 次比较操作。
- 当 ( i = 1 ),内层循环进行 ( n - 2 ) 次比较操作。
- 依此类推,直到 ( i = n - 2 ),内层循环进行 1 次比较操作。
总比较次数为:
因此,总时间复杂度为 ( O(n^2) )。
2. 空间复杂度
选择排序的空间复杂度为 ( O(1) )。它只使用了固定的额外空间来存储交换操作,并不依赖于输入数组的大小。
五、算法的优点
- 简单易懂:选择排序是一种简单直观的排序算法,容易理解和实现。
- 原地排序:选择排序不需要额外的存储空间,只使用原始数组进行排序。
- 适用于小型数组:对于小型数组,选择排序的性能表现较好。
六、算法的缺点
- 时间复杂度高:在处理大规模数据时效率较低。
- 不稳定:选择排序在排序过程中可能会改变相同元素的相对顺序,因此它是一种不稳定的排序算法。
七、优化方案
选择排序的时间复杂度为 ( O(n^2) ),在处理大规模数据时效率较低。可以考虑以下优化方案:
使用线段树:每一个内层循环是从一个区间中找到一个最小值,并且更新这个最小值。这个过程可以通过使用线段树将时间复杂度优化为 ( O(\log n) ),从而使总的时间复杂度变为 ( O(n \log n) )。
堆排序:堆排序是一种更为高效的选择排序优化方法,后续可以进一步学习和应用。
通过以上优化,可以显著提升选择排序在大规模数据处理中的性能。